Numerical Analysis | Ioannis Koutalios

Cover Image by Mika Baumeister on Unsplash

This page contains some of the projects I have done in the field of numerical analysis, as part of my coursework during my undergraduate and graduate studies. The page is still under construction and will be updated as I add more projects.

Numerical Methods

The following projects were part of the Numerical Methods course I took during my undergraduate studies. The projects were done in C++ and Mathematica. The code is available in my GitHub repository, with instructions on how to compile and run it. Below is a brief description of each problem and the results.

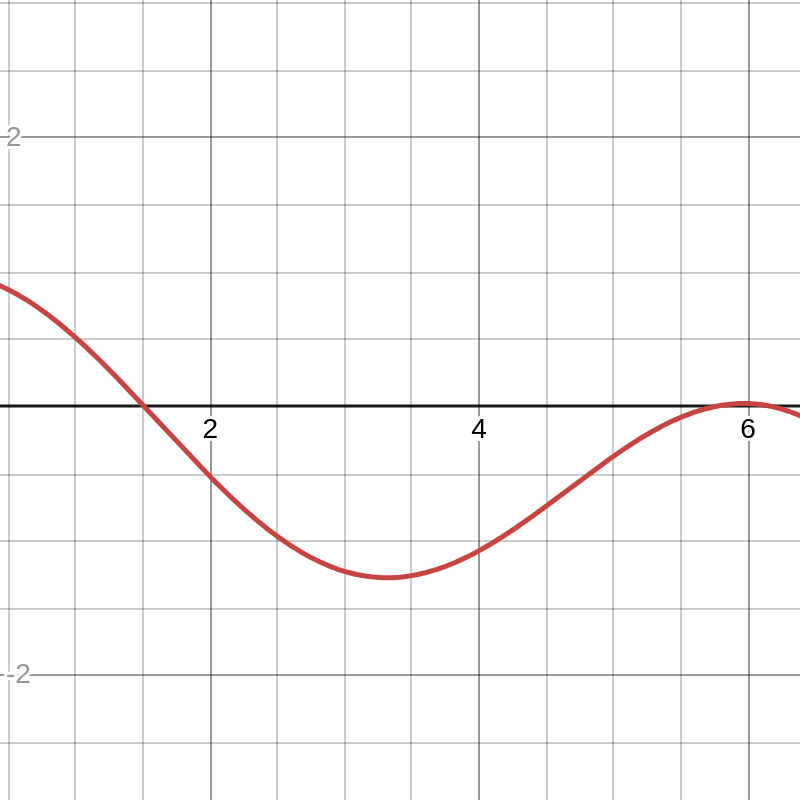
The first set of problems was about solving equations using fixed-point iteration and Newton-Raphson methods. The equations that needed to be solved were: \begin{equation} f(x) = \cos(x) - 0.026x^2 = 0 \label{eq:1} \end{equation} for x>0.

We used the $x=g(x)$ method (fixed-point iteration) to solve the equation. We simplified the equation to the form $x=g(x)$ and selected a starting point to iterate the function until we reached the desired accuracy. We also used the Newton-Raphson method to find the roots of the equation. The Newton-Raphson method uses the formula: \begin{equation} x_{n+1} = x_n - \frac{f(x_n)}{f’(x_n)} \end{equation}

The \eqref{eq:1} equation has 3 roots, which we tried to find using both methods.

With the Newton-Raphson method, we found all 3 roots of the equation, while with the fixed-point iteration, we found the first and third roots.

We also had to solve the system of equations: \begin{equation} -2x^3 + 3y^2 + 42 = 0 \end{equation}

\[5x^2 + 3y^3 - 69 = 0\]

The system has one real solution, which is $(x, y) = (3, 2)$. We used the Newton-Raphson method to find the solution to the system of equations. The implementation of the method was correct, but the method did not converge to the solution.

Left: The graph of the function $$f(x) = \cos(x) - 0.026x^2$$. The roots of the function are the points where the function crosses the x-axis. We can see that the function has 3 roots in the interval we are interested in. Right: The function $$f(x) = 3x e^x - e^{2x}$$ (red) compared to the Lagrange polynomial (blue) and the Hermite polynomial (grey). For the Lagrange polynomial, we used the points (0, -1), (1, 0.765789), (2, -10.263813). For the Hermite polynomial, we only used the last two points. We can see that the Hermite polynomial is a better approximation of the real function.

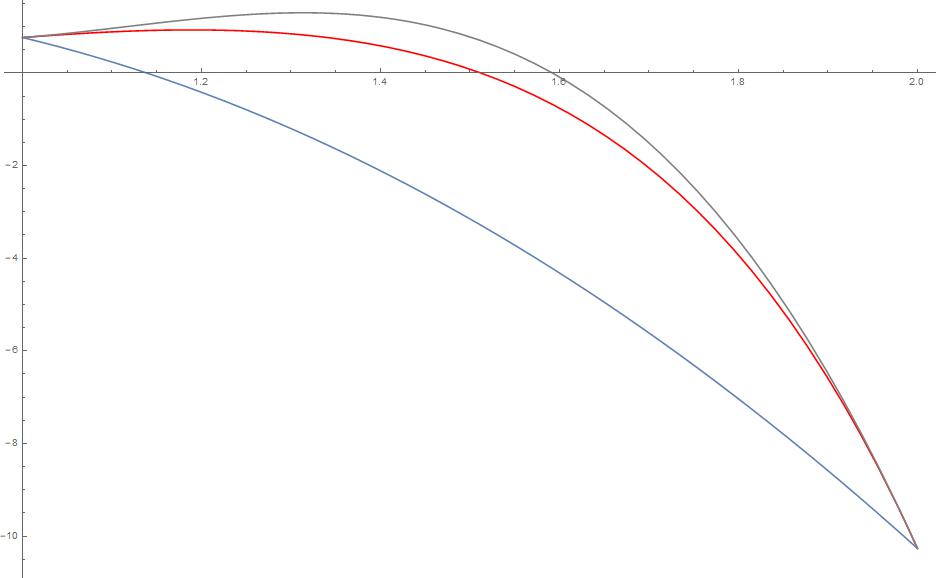
The second set of problems was about solving the system of equations using the Gauss-Seidel method. The system of equations was:

\[4x + 3y = 24\]

\begin{equation} 3x + 4y - z = 30 \end{equation}

\[-y + 4z = -24\]

We used the Gauss-Seidel method to solve the system of equations. The starting point was $x_0 = (1, 1, 1)$. The code found the solution to the system of equations $x = 3, y = 4, z = -5$.

We also had to find the Lagrange polynomial for the following points: \begin{equation} (0, -1), (1, 0.765789), (2, -10.263813) \end{equation} which are part of the function $f(x) = 3x e^x - e^{2x}$. We can also find the Hermite polynomial for the last two points.

The Lagrange polynomial is a polynomial that passes through all the points given. The Hermite polynomial is a polynomial that passes through the points and has the same derivative as the function at the points.

The third set of problems was about calculating integrals using the Simpson’s rule. We had to calculate the following integrals: \begin{equation} \int_{0}^{3} \frac{1}{5x^2 + 1} dx \end{equation} and \begin{equation} \int_{0}^{2\pi} e^{-x/4} \sin(20x) dx \end{equation}

The Simpson’s rule is a method for numerical integration that approximates the integral of a function as the sum of the areas of a series of trapezoids. The code found the value of the first integral to be $0.636301999167$ and the value of the second integral to be $0.039599888602$. The code used $n = 31$ subintervals for the first integral and $n = 999$ subintervals for the second integral. We notice that for the second integral, a very high number of subintervals is needed to get an accurate result. This is because the function oscillates very quickly, and the Simpson’s rule is not very accurate for such functions.

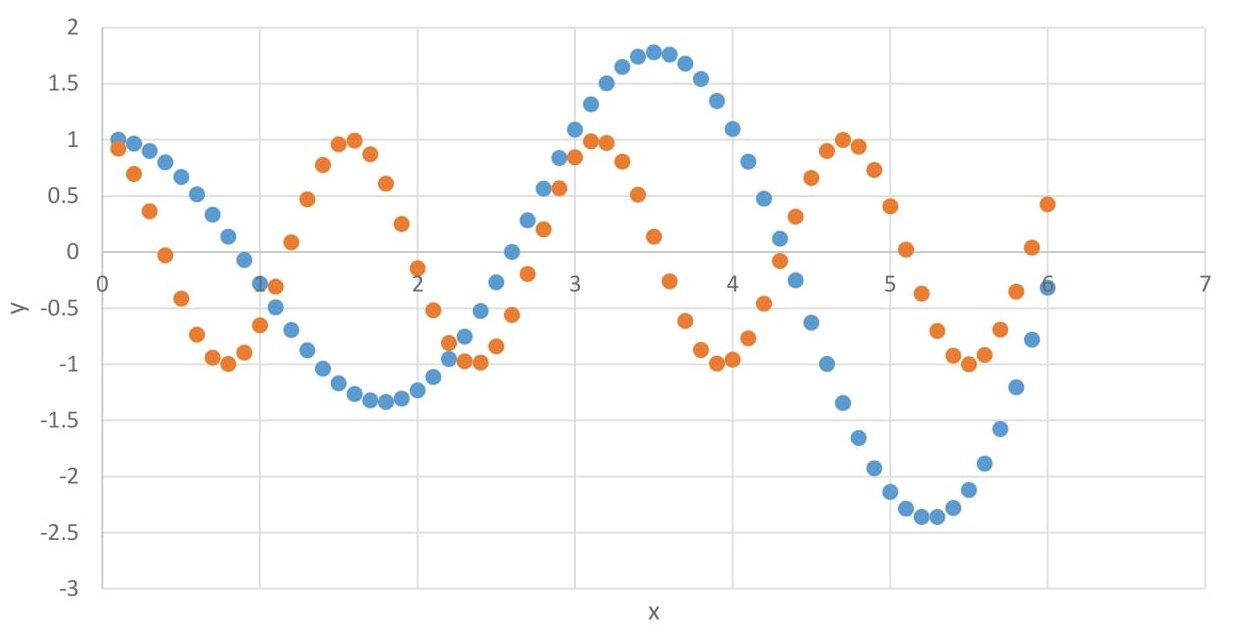
The fourth set of problems was about solving differential equations using the Runge-Kutta method. We had to solve the following differential equation: \begin{equation} y’’ + \omega^2 y = 0 \end{equation} where $\omega = 4$ and $y(0) = 1, y'(0) = 0$.

We used the Runge-Kutta method of order 2 and 4 to solve the differential equation.

The solutions to the differential equation using the Runge-Kutta method of order 2 (left) and 4 (right). The orange line is the real solution, and the blue line is the approximated solution.

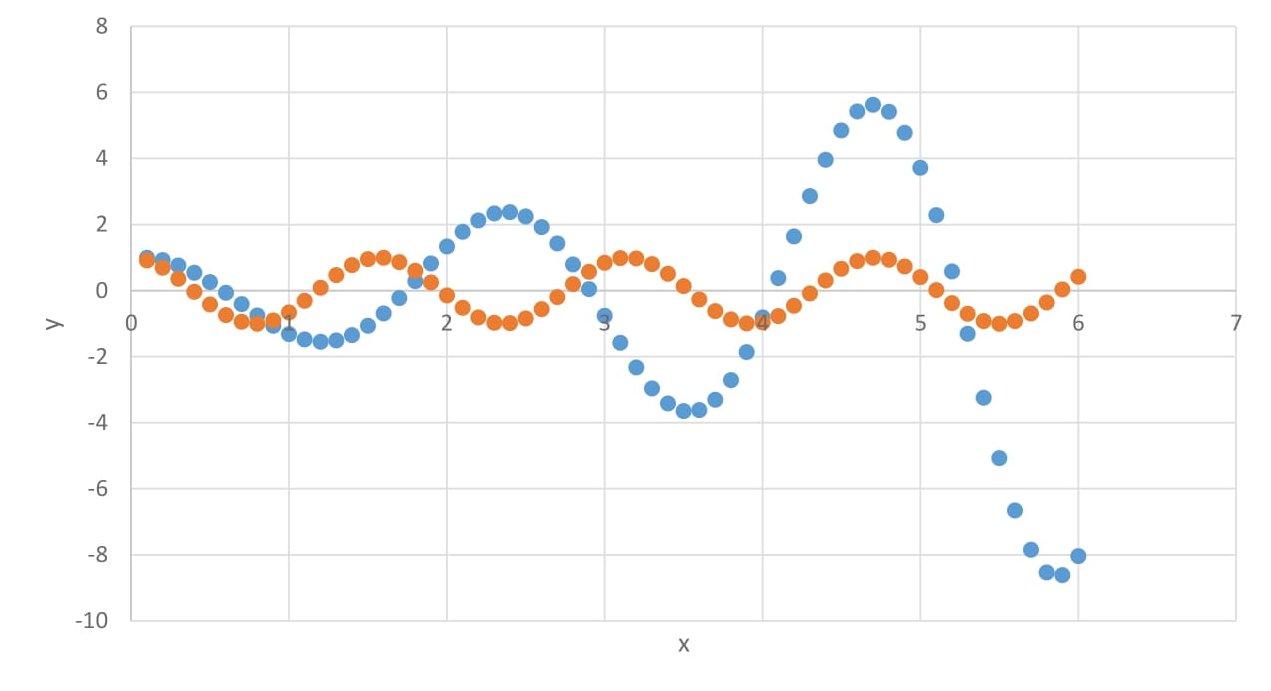
We also had to solve the following differential equation: \begin{equation} y’ = -10 \frac{y^2}{x} \end{equation} where $y(0.1) = 1$.

We used the shooting method to solve the differential equation. The code used the Runge-Kutta method of order 2 to solve the differential equation. The values of y get to infinity, which is not correct, but was the intended result, to show that the method does not converge.

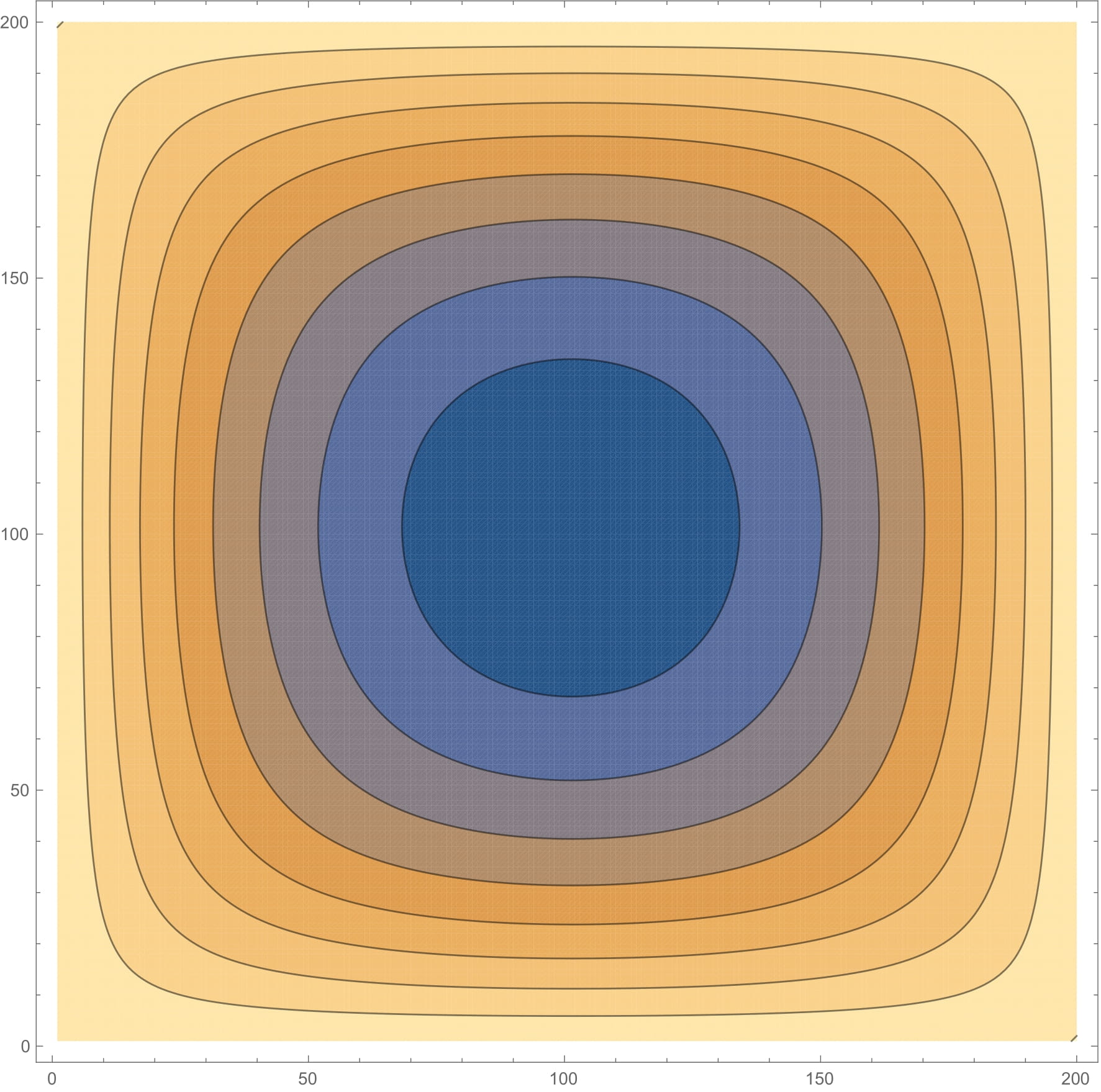
The fifth set of problems was about solving boundary value problems using the Liebmann method and the wave equation using the Lax-Wendroff method. We had to solve the following boundary value problem: \begin{equation} u_{xx} + u_{yy} = 10.0e^{-0.5(\sqrt{(x-0.5)^2 + (y-0.5)^2})} \end{equation} with the boundary conditions: $u(x, y) = 1.0$ in all the boundaries.

The Liebmann method is an iterative method for solving the boundary value problem. The results can be visualized by plotting the values of the output matrix.

The solution to the boundary value problem using the Liebmann method (left) and the solution to the wave equation using the Lax-Wendroff method (right).

We also had to solve the wave equation: \begin{equation} u_{tt} - \alpha^2 u_{xx} = 0 \end{equation} with $\alpha^2 = \frac{2}{\pi^2}$ in the interval $0 \leq x \leq 12$ and with the initial conditions: $u(x, 0) = \sin(\pi x)$ for $2 \leq x \leq 4$ and $u(x, 0) = 0$ for $0 \leq x < 2$ and $4 < x \leq 12$ and the boundary conditions: $u(0, t) = 0$ and $u(12, t) = 0$.

The Lax-Wendroff method is a method for solving the wave equation. It is a finite difference method that approximates the solution to the wave equation. The wave equation can be solved by iterating the method for different time steps.